Welcome to CBT2CBT!

Introduction to Gradient Descent

Details

Hits: 421

Introduction to Gradient Descent

These are some of the solutions that is made simple when working with cloud solutions

--------------

Gradient Descent is an optimization algorithm used for minimizing a function by iteratively moving towards the steepest descent, as defined by the negative of the gradient. This method is widely used in machine learning for finding the optimal parameters for models. By adjusting the parameters in the direction of the negative gradient, Gradient Descent ensures that the loss function is minimized, leading to better model predictions. One of the key equations in Gradient Descent is the parameter update rule, given as:

--------------

Gradient Descent is an optimization algorithm used for minimizing a function by iteratively moving towards the steepest descent, as defined by the negative of the gradient. One of the key equations in Gradient Descent is the parameter update rule:

--------------

θ_t+1 = θ_t - α θ_t)

--------------

Where:

• θ represents the parameters being optimized.
• α is the learning rate, which controls the size of the steps taken.
• &nabla L(θ) is the gradient of the loss function with respect to the parameters.

Alternative rendering

$$ \theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t) $$

Where:

• θ represents the parameters being optimized.
• α is the learning rate, which controls the size of the steps taken.
• ∇L(θ) is the gradient of the loss function with respect to the parameters.

-------- Note that there may be some HTML representation missing in the above formular ------

Methods of Delivering Services

Details

Hits: 278

Services and background tasks:

Methods of Delivering Services: Understanding Backpropagation

In modern AI services, one of the most effective methods for optimizing deep learning models is through the process of Backpropagation. Backpropagation is the core algorithm used to train neural networks. It works by propagating the error backward through the network, adjusting the weights to minimize the difference between the predicted output and the actual output.

To understand Backpropagation in the context of neural networks, consider the following key formulas used during the weight update process:

The weight update rule for a given layer is given by:

$$ w_{ij}(t+1) = w_{ij}(t) - \eta \frac{\partial L}{\partial w_{ij}} $$

Where:

• w_ij represents the weight between neuron i in the previous layer and neuron j in the current layer.
• η is the learning rate, controlling the step size of the weight update.
• L represents the loss function, which measures the difference between the network's output and the expected output.
• ∂L/∂w_ij is the partial derivative of the loss with respect to the weight w_ij.

In Backpropagation, we also need to compute the error at each layer. For the output layer, the error δ is calculated as:

$$ \delta_j = (y_j - \hat{y}_j) \cdot \sigma'(z_j) $$

Where:

• y_j is the actual output.
• ĥy_j is the predicted output of the network.
• σ'(z_j) is the derivative of the activation function applied to the input z_j.

Once the error is calculated for the output layer, it is propagated backward to update the weights of the hidden layers. The error term for the hidden layer is given by:

$$ \delta_j = \sigma'(z_j) \sum_k \delta_k w_{jk} $$

In this equation:

• σ'(z_j) is the derivative of the activation function.
• δ_k is the error term for the next layer.
• w_jk represents the weight between the current layer and the next layer.

The process of Backpropagation allows the network to fine-tune its weights iteratively, reducing the error and making better predictions over time. This method is crucial for delivering AI-powered services, such as recommendation systems, image recognition, and natural language processing.

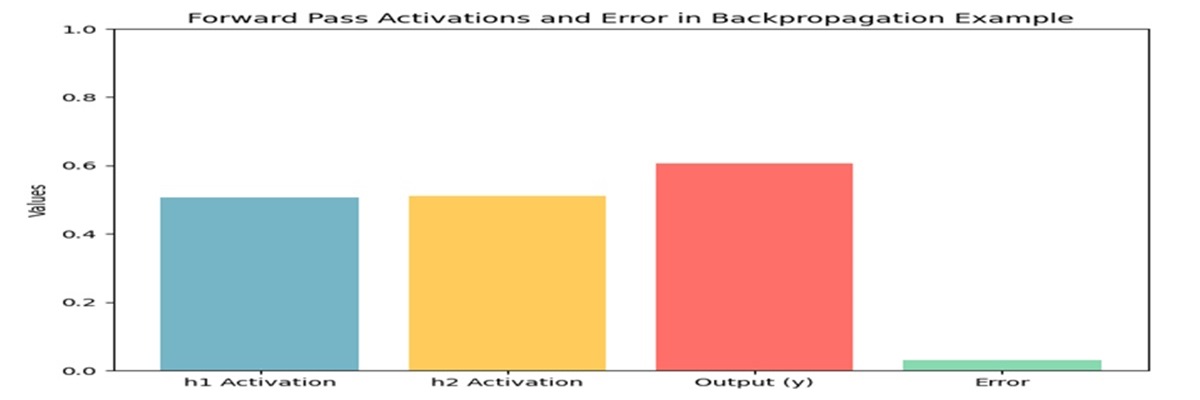
Backpropagation with Sample Data

Details

Hits: 386

Sample Example: Backpropagation Example:

The following imports are require for running the script in Python

• import numpy as np
• import matplotlib.pyplot as plt

 

Step 1: Initialize Weights and Inputs

$$ w_{1} = 0.15, \quad w_{2} = 0.20, \quad w_{3} = 0.25, \quad w_{4} = 0.30 $$ $$ w_{5} = 0.40, \quad w_{6} = 0.45 $$ $$ x_{1} = 0.05, \quad x_{2} = 0.10 $$

Step 2: Forward Pass (Calculate Activation)

$$ h_{1} = \sigma(w_{1}x_{1} + w_{2}x_{2}) = \sigma(0.0175) $$ $$ h_{2} = \sigma(w_{3}x_{1} + w_{4}x_{2}) = \sigma(0.0275) $$ $$ y = \sigma(w_{5}h_{1} + w_{6}h_{2}) = \sigma(0.75) $$

Step 3: Calculate Loss (Mean Squared Error)

$$ L = \frac{1}{2} (0.85 - 0.75)^2 = 0.005 $$

Step 4: Backpropagate Error

$$ \delta_{\text{output}} = (t - y) \cdot \sigma'(z_{\text{output}}) $$ $$ \delta_{\text{output}} = (0.85 - 0.75) \cdot 0.18 = 0.018 $$

Step 5: Update Weights

$$ w_{5} = w_{5} + \eta \cdot \delta_{\text{output}} \cdot h_{1} $$ $$ w_{6} = w_{6} + \eta \cdot \delta_{\text{output}} \cdot h_{2} $$

-------- Note that there may be some HTML representation missing in the above formular ------

This link takes you to the conversation so you can make your voice heard on Cloud Base Training Forum.

Ai and ML are not new but they make an interesting concept in Technology. Login to run the script that generated the above graph

Goto to Forum.

Back Top